
Capacity Testing
A.J. Erickson, P.T. Weiss, J.S. Gulliver, R.M. Hozalski, B.C. Asleson
After visual inspection has been performed and there are no obvious malfunctions, capacity testing should be considered if infiltration or sedimentation capacity is an important function of the stormwater treatment practice. Capacity testing is an assessment method used to determine either the hydraulic conductivity or the sediment accumulation capacity (sediment storage volume) of the stormwater treatment practice from a number of spatially distributed, relatively rapid point measurements. The point measurements are distributed spatially to estimate the overall hydraulic conductivity or sediment retention capacity of the stormwater treatment practice. Capacity testing protocols for other functions, such as chemical retention of stormwater treatment practices, have not yet been developed.
The procedure for capacity testing (level 2) varies for each stormwater treatment practice and assessment goal. Therefore, the reader should consider the recommendations located in each of the Filtration, Infiltration, Sedimentation, and Biologically Enhanced Practices sections of this manual. As with any field work, safety is an important concern and should be addressed when conducting capacity testing.
Infiltration capacity tests
Infiltration capacity testing is a method of capacity testing that produces an estimate of the overall hydraulic conductivity of a stormwater treatment practice using a network of point measurements. Hydraulic conductivity is measured at a number of locations in the stormwater treatment practice and recorded with the corresponding spatial location. The hydraulic conductivity is then spatially averaged (geometrically) to estimate the overall hydraulic conductivity for the stormwater treatment practice. The overall hydraulic conductivity can be used to predict the rate at which water will infiltrate into the soil or filtrate through the filter media, which can help determine if an infiltration or filtration practice needs maintenance or repair.
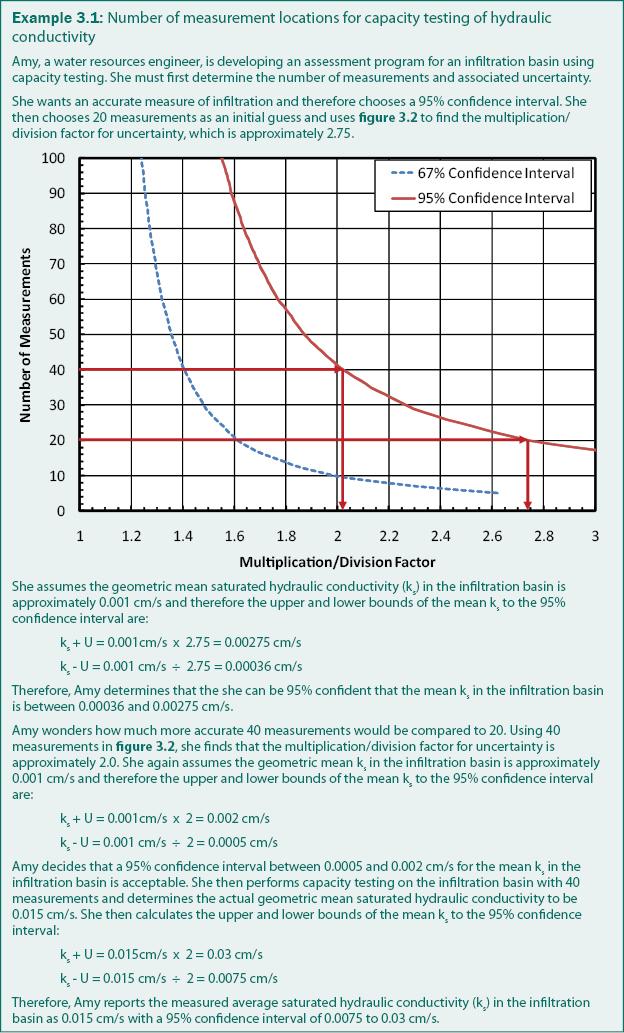
The accuracy of infiltration capacity tests is dependent on the number of point measurements and the spatial mean and variance of the measurements. Measurements of hydraulic conductivity in rain gardens have been used to develop a relationship between measurement uncertainty and the number of measurements required for estimating saturated hydraulic conductivity (Asleson et al. 2009), as shown in figure 3.2.
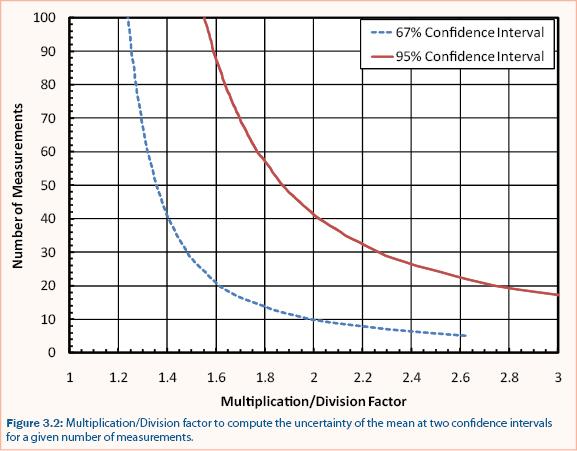
Measurement uncertainty can be expressed by the confidence interval which represents the range within which the actual mean will be included based on a number of samples for a given level of confidence (e.g., 95%). Confidence intervals for normally distributed populations can be calculated from equation 7.17 (repeated here) if the standard deviation, number of samples, and Student (Gosset) t value is known.
To simplify application of equation 7.17 to infiltration capacity testing, the standard deviation of saturated hydraulic conductivity can be estimated from measurements. Saturated hydraulic conductivity was measured in 178 locations within various rain gardens throughout the Minneapolis/St. Paul metropolitan area (Asleson et al. 2009). The measurements were assumed to be log-normally distributed.
First the measurements were log-transformed. The mean and standard deviation of these log-transformed measurements (log-mean and log-standard deviation, respectively) was estimated from several randomly sampled sets of sample size (n) between 5 and 100 from the 178 measurements. The mean and standard deviation of the log-means was estimated from these randomly collected sets each sample size (n). This standard deviation was used in equation 7.17 along with the Student (Gosset) t value (for α = 0.33 and α = 0.05) and number of measurements (n) to determine the uncertainty of the log-mean. The multiplication/division factor was then determined by equation 3.3.
The uncertainty in saturated hydraulic conductivity measurements can be estimated (assuming log-normally distributed measurements) by multiplying (or dividing) the geometric mean (see equation 3.1) by the multiplication/division factor (multiplication = mean + uncertainty; division = mean - uncertainty). The geometric mean is used because calculating the geometric mean does not require log transformation and because the geometric mean is equal to the mean of the log-transformed measurements if the data is log-normally distributed.
This relationship can be used to determine the uncertainty that will result from a given number of hydraulic conductivity measurements as follows:
- Choose an initial guess for the number of measurements (e.g., 10)
- Choose the level of confidence (e.g., 95% confidence interval)
- Use figure 3.2 to determine the multiplication/division factor for uncertainty
- Decide whether the uncertainty is acceptable
- Take measurements of hydraulic conductivity
- Compute the geometric mean of the measurements using equation 3.1
- Estimate the uncertainty in the measurements as demonstrated in example 3.1.

Two confidence intervals are provided in figure 3.2; 67% and 95%. The 95% confidence interval is recommended to adequately represent uncertainty in saturated hydraulic conductivity because it indicates that there is a 95% probability that the actual mean saturated hydraulic conductivity will be within the confidence interval. If the constraints of the assessment program limit the number of measurements, then the 67% confidence interval can be used and should be reported with the measured values as demonstrated in example 3.1.
Several devices are available to determine soil hydraulic conductivity and most of these devices have been evaluated as described in Infiltration. The Modified Philip-Dunne infiltrometer (figure 3.3) is recommended for estimating saturated hydraulic conductivity of the top 30 cm (12 inches) in the field.

Infiltration capacity tests can be performed on the following stormwater treatment practices: dry ponds, bioretention practices (rain gardens), sand or soil filters, infiltration trenches, infiltration basins, filter strips, and swales. Hydraulic conductivity in stormwater treatment practices may vary based on climatic season, soil conditions, etc., and therefore hydraulic conductivity tests should be performed at several different times throughout the year to get an overall estimation of hydraulic conductivity. An example schedule for hydraulic conductivity tests could include testing in the spring after the ground thaws, in mid-summer, and in late fall before the ground freezes.
Small infiltration rates as identified by infiltration capacity tests may be attributed to clogging of the surface layer with captured sediments or a relatively impermeable subsurface layer. A soil core can be examined for the presence of relatively impermeable layers to determine the cause of small hydraulic conductivity.
An advantage of infiltration capacity tests as compared to synthetic runoff testing (level 3) is that it can be performed for all sizes of stormwater treatment practices. Synthetic runoff testing is dependent upon an adequate supply of synthetic runoff, which limits its use to smaller stormwater treatment practices. The advantage of capacity tests compared to monitoring (level 4) is that less time and expense is required to perform the assessment. Another advantage is the ability to evaluate maintenance procedures because the cause of reduced infiltration capacity can be easily identified using capacity testing. Also, specific locations within the stormwater treatment practice with small (or excessively large) infiltration capacity can be identified with capacity testing. If identified, these locations can be repaired as opposed to the entire practice, saving both time and money. Infiltration capacity testing conducted annually can also be used to estimate the change in hydraulic conductivity with respect to time (e.g., Δ inches/year).
Sediment accumulation tests
Sediment accumulation tests estimate the sediment accumulated in a stormwater treatment practice. Using surveying equipment or GPS units, sediment surface elevation measurements are taken throughout the stormwater treatment practice and the data are entered into three-dimensional drafting software (e.g., AutoCAD, Microstation). For manholes or proprietary devices, only a few measurements may be required because the area is small. The data can then be compared to similar data of initial surface elevation measurements to determine the amount of sediment that has accumulated. The amount of accumulated sediment can then be compared to the design sediment storage volume to determine the available capacity for additional sediment capture. Sediment accumulation tests therefore require as-built plans or topographical data obtained as recently after construction as possible to determine the initial surface elevation. The rate of sediment accumulation can also be calculated for a given time period using equation 3.2.

Sediment accumulation tests can be applied to any stormwater treatment practice that collects sediment and allows sediment surface elevations to be measured. Sediment accumulation tests can be performed on dry ponds, wet ponds, wetlands, wet vaults, and underground proprietary devices.
A major advantage of capacity testing (level 2) for sediment accumulation as compared to synthetic runoff testing (level 3) is that it can be performed for all sizes of stormwater treatment practices. Synthetic runoff testing is dependent upon an adequate supply of synthetic runoff, which restricts its applicability to smaller stormwater treatment practices. Compared to monitoring (level 4), capacity testing (level 2) for sediment accumulation requires less time and are less expensive to perform. Another advantage is the ability to use sediment accumulation as a diagnostic test for maintenance procedures because the source of the accumulation can be more easily identified.
Testing conducted annually can be used to estimate the sediment accumulation rate with respect to time (e.g., lbs/year). Sediment accumulation testing cannot be used, however, to assess pollutant removal efficiency because it only measures the amount of sediment captured and does not measure the amount of sediment entering and exiting a stormwater treatment practice. Therefore, if the assessment goals include pollutant removal efficiency, synthetic runoff testing (level 3) or monitoring (level 4) must be considered.
Continue to Synthetic Runoff Testing (level 3).


